これの後編です。待たせたな！！(誰も待ってない)

前回のあらすじ

読んでいない人は前編から読んでくれよな！←

キューブのあり得る状態数が知りたくなった
8個のコーナーと12個のエッジを適当に配置する方法は519,024,039,293,878,272,000通りもあるが、あり得る状態はそのうち一部だけ
操作に関する不変量が3つ( $sgn(x), pivot(x), flip(x)$ )存在し、これが完成状態と一致しない配置はあり得ない状態
それらが独立であることから、あり得る状態が高々43,252,003,274,489,856,000通りしかないことが示される
$sgn(x)=1,pivot(x)=flip(x)=0$ である状態 $x$ が揃えられることを示せば証明全体が完結する
揃えられることを示すには揃える方法を提示するしかない

というわけで、後編はキューブの揃え方の構築となります。

キューブの解法汎論

冒頭に述べた通りキューブを揃えるのは難しいです。段階的にキューブを揃えていく上で何が難しいかというと、次に揃えたい部分を揃えると既に揃えた部分が崩れてしまうことです。(当たり前すぎですね)

その解決のために、一般にキューブの解法と呼ばれているものは、大抵*1

既に揃えた部分を維持しながら残りの状態を変えるような操作をいくつか考え、それらの組み合わせによって目的部分を揃える

ということの繰り返しになっています。

では既に揃えた部分を維持するような操作はどうやって見つけるのかというと、気合です。言い方を変えれば全探索です*2。当然ながら、ステップが進めば進むほど"既に揃えた部分を崩さない"という制約は厳しくなり、それを満たす操作は長く複雑になる傾向があります。キューブを何も見ずに揃えられるようになるということは、それらの複雑な手順を暗記するということに他なりません。巷で"初心者でも簡単に覚えられるキューブの解法"として示されているものでも、7手以上の操作を少なくとも5つくらいは暗記することを要求しています。長い操作は12手以上にも及びます。

確かに上記のような一般的な解法の一つを述べればこの命題は解決されるのですが、それでは数学的に面白くない。『がんばって探索したらできました』というのは数え上げ問題の解答として美しくない！！

…という筆者の謎のプライドにより、今回は非自明な(暗記すべき)手順というものを極力廃した、本当にすぐに覚えられる解法というものを説明してみたいと思います。といってもこれは全然自分のオリジナルではなく、台湾のReheart Sheuという方が開発した8355 method*3というものをベースにしています。気になる方は検索してみてください。

1時間で分かるキューブの解法

ということでやっていきます。必ず揃えられることの証明に重点をおきたいので、巷の解法解説よりやたらと長くなることが想定されますが、ご容赦ください。

一応「証明」という側面をハッキリさせたいので、今から示す命題を改めて書いておこうかと思います。「仮定」を使う部分が今後かなり長い間出てこない*4ので忘れないように、という意味合いもあります。

$Thm.$ $\,\,sgn(x)=1,pivot(x)=flip(x)=0$ である状態 $x$ は正規の手段を使って揃えられる。

基礎手順RUR'U'

8355 methodの根底にあるのが、前編で述べた回転記号でRUR’U’と表される操作の特性です。たった4手ですが、非常に面白い特性を備えている操作です*5。以降多用するので、この操作をSと呼ぶことにしましょう*6。
回し方の参考？

R面を奥に
U面を右人差し指で引く
R面を手前に
U面を左人差し指で引く

操作Sの性質は以下の通りです。

Sで位置や向きが変化するのは下図において色がついたパーツだけである。灰色のパーツの位置と向きは変化しない。
Sによって赤色のコーナー2つの位置が入れ替わる。Sを2回行うとこれらの位置は元に戻るが向きが変わっている。Sを6回行うと位置も向きも元に戻る。この間に2つのコーナーは全ての位置と向きの組み合わせ( $2\times 3=6$ 通り)を1度ずつ通る。
Sによって青色のコーナー2つの位置が入れ替わり、赤色のコーナー2つと同様2回では元に戻らず6回で元に戻る。
Sによって黄・緑色がついたエッジ3つの位置が巡回的に入れ替わる。このとき黄色い面は黄色い面に移り、Sを3回行うとこれらのエッジは位置も向きも元に戻る。

f:id:goldenfalcon496:20191209214711p:plain — 操作Sに影響される部分

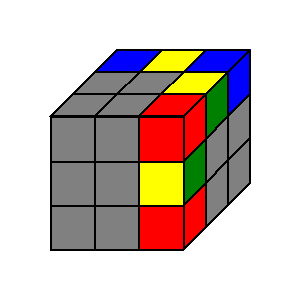
なお、前編で述べた「位置の記法」を用いれば操作Sによるパーツの移動を以下のようにカッコよく書くことができます。(向きに注意。)

$UFR\mapsto RFD\mapsto RUF\mapsto DRF\mapsto FRU\mapsto FDR\mapsto UFR$
$URB\mapsto UBL\mapsto RBU\mapsto BLU\mapsto BUR\mapsto LUB\mapsto URB$
$FR\mapsto UR\mapsto UB\mapsto FR$

また、この操作の完全な鏡映であるL'U'LUもほぼ同様の鏡映しになった性質を持っています。こちらはSSとでも呼ぶことにしましょう。この特性を巧みに使って、というか酷使してなんとかキューブを揃えていきます。

1.D面エッジを揃える

とは言いましたが最初の最初はSなんぞ使わずにやります。簡単すぎて逆に書きづらいのですが、アルゴリズム風に書いてみます。

D面色を含むエッジ $X$ で、揃っていない(正しい位置・向きになっていない)ものをとる
の位置で場合分け:
- がUorD面に属さないとき、ある側面(U,D以外の面)を90度回転させればを正しい向きでD面のある位置に移動できる。が入るべき位置をとして、
  - $L _ X$ のエッジが $L$ に移動するようD面を回転
  - $X$ を $L$ に移動
  - $L$ のエッジが $L _ X$ に移動するようD面を回転
  - すると $X$ は正しい向きで $L _ X$ に入る。
- がD面に属するとき、
  - $X$ が属する側面を90度回転すると $X$ はUorD面に属さない位置に移動する。
- がU面に属するとき、を含む側面を90度回転させるとUorD面に属さない位置に移動できるが、真下にあるエッジが崩れる恐れがある。そこで、が入るべき位置を、の真下のエッジの位置(D面に属する)をとして、
  - $L _ X$ のエッジが $L$ に移動するようD面を回転
  - $X$ を含む側面を90度回転
  - $L$ のエッジが $L _ X$ に移動するようD面を回転
  - すると(既に揃ったD面のエッジは崩れず) $X$ はUorD面に属さない位置に移動する。

書き下すと無駄が多いですが、D面のエッジが4つ揃うはずです。この辺は揃えられることの証明といっても当たり前なのですが、一応必ず揃う方法の提示をしました。

2.D面コーナーを3つ揃える

操作Sの特性を生かしてD面コーナーを3つ揃えます。4つ揃えることもできますが、後で崩れるので3つで十分です。

D面色を含むコーナー $X$ で、揃っていないものをとる
の現在の位置で場合分け:
- がU面にあるとき、
  - $X$ が入るべき位置を $L _ X$ とする
  - D面を下向きに維持しながらキューブ全体の向きを変えて $L _ X$ が位置DFRに来るようにする
  - $X$ が位置UFRに来るようにU面を回転
  - Sを繰り返すと、Sの性質より6回以内に $X$ が正しい向きと位置で入る
  - (このとき、Sの性質により他のD面パーツは崩れない)
- がD面にあるとき、
  - D面を下向きに維持しながらキューブ全体の向きを変えて $X$ が位置DFRに来るようにする
  - Sを1回行うと、 $X$ がU面に来る
  - (このとき、Sの性質により他のD面パーツは崩れない)

コーナーが全ての向きを通って入れ替わる、D面はDFR以外変化しないというSの性質が使われています。よくある解法では向きによる場合分けがなされ総当たり性(?)が増していますが、この方法では「繰り返せばいつか揃う」の一言で済みます*7。DFR以外のD面が崩れないので、すでに揃えた部分は保存されます。

D面を下向きに維持しながらキューブ全体の向きを変えるという操作はキューブの解法に頻繁に登場します。以降、この操作のことを持ち替え*8と呼ぶことにします。
また、D面コーナーのうち(現時点で)揃っていないものを $K$ と呼ぶことにします。今後しばらくは、 $K$ 以外のD面パーツは崩してはいけないが、 $K$ だけは崩してもよいという制約で揃えていきます。 $K$ は最後に揃えます*9。

3.中段エッジを(3つ)揃える

中段というのはU面にもD面にも属さない部分のことです。すなわち、このステップのターゲットはFR、RB、BL、LFの4つのエッジです。ただし、 $K$ の真上にあるエッジは後で崩れるので、揃える必要はありません。操作Sで $UB \mapsto FR$ と(U面から中段に)エッジが移動するのを利用したいのですが、「エッジは向きを保って動く」というSの特性により、向きが合っていない場合Sだけでは揃えられません。そこで、鏡映である操作SS( $=L’U’LU$ )も使っていきます。
詳しくは(長い)→*10

中段に入るべきエッジ $X$ で、揃っていないものをとる
の現在の位置で場合分け:
- がU面にあるとき、
  - $X$ が入るべき位置がRFに来るよう持ち替え
  - $K$ がRFDに来るようD面を回転
  - の2面のうちU面を向いた面の色が現在のF面色と一致しているならば、
    - $X$ がUBに移動するようU面を回転
    - Sを行う(D面は $K$ のみ崩れる)
  - 一致していないならば、
    - RFがLFに来るよう持ち替え
    - $X$ がUBに移動するようU面を回転
    - (この時点で $X$ のU面がF面色に一致する)
    - SSを行う(D面は $K$ のみ崩れる)
- が中段にあるとき、
  - $X$ がRFに来るよう持ち替え
  - $K$ がRFDに来るようD面を回転
  - Sを行う(D面は $K$ のみ崩れる)
  - すると、 $X$ がU面に移動する
(最後にD面を回転させ $K$ を元の位置に戻す)

実行してみると、 $K$ を犠牲にして(?)上手く揃えていることが分かると思います。
なお、D面部分だけを持って上の2段を回転*11させることで、持ち替え+D面回転と等価な操作ができます。慣れて来るとこちらの方が手早く揃えられてカッコいいです。

ここまでの手順で、だいぶ揃ってきた感があると思います。揃っていないのはU面のパーツと $K$ 、および $K$ の真上のエッジだけになっているはずです。以降、 $K$ の真上のエッジを $E$ と呼ぶことにしましょう。

4.U面エッジを揃える

佳境に入ってきました。おそらくここが一番難しいステップです。

(1)向きを揃える

まずはU面エッジの向きを揃えます。U面色を持つエッジが全てU面にあり、かつU面色が上を向いている状態(位置は問わない)が目標です。俗に(?)「十字を揃える」と呼ばれます。
若干ややこしいので揃える方針を先に述べておきます。揃っていないU面エッジを一旦 $E$ へ送り、SとSSを使い分けることで正しい向きでU面に戻すという構想ですが、標的パーツを一旦 $E$ に送るところで $E$ がU面に出てくるので、これが逆向きで入ってしまうと本末転倒です。そこで、

揃っていないU面エッジを $E$ に取り込む
$E$ のエッジを正しい向きでU面へと送りだす

以上の2つを同時に行うことで揃えていきます。U面色を含まない(最終的に $E$ に収まるべき)エッジの向きは特に気にする必要はありません。では具体的手順へ。

以下を繰り返す
- のエッジによって場合分け:
  - U面色を持つとき、 $E$ がFRまたはFLに来て、かつF面にU面色が見えるように持ち替え
  - U面色を持たないとき、 $E$ がFRに来るよう持ち替え(実際どちらでもよい)
- U面の状況によって場合分け:
  - 向きの揃っていないU面エッジがあるとき、それがUBに来るようU面を回転
  - 揃っていないU面エッジがないとき、U面色を持たないエッジがUBに来るようU面を回転
  - (それもない場合、既に目標状態になっている)
- $E$ がFRならばS、FLならばSSを行う
- すると、 $X$ が $E$ に入り元々 $E$ であったエッジは(U面色を持つならば)正しい向きで入る
- (Sの性質より既に揃えた部分は崩れない)

繰り返すごとに揃っていないエッジが必ず減っていくので、いつか十字が完成することは簡単に示せます。

(2)位置を揃える

U面エッジ4つが正しい向きで入りましたが、位置が合っていません。ただ、一見合っていないように見えてもU面を回転したら揃っていた…という場合もあります。以下、しばらく理論っぽいことを書きますが、結局総当たり的なので、最悪飛ばしてもらっても結構です。
まずはどのような状況があり得るのかを考えてみます。1つのエッジを正しい位置に合わせると、残り3つのエッジは全て合っているか、1つ合っていて残り2点交換になっているか、全て合っておらず3点交換になっているかのいずれかです。さらに少し考えると、3点交換に見える配置は基準点を変えることで隣接2点交換にも見えるということが分かります。以上をまとめると、(揃っている場合を除いて)状況は以下の2つのケースしかありません。

ケース1. 隣接2点交換⇔3点交換
ケース2. 対面2点交換

ここからSを駆使してU面エッジを入れ替えていきたいのですが、結論から言うとSではU面の2点交換は直ちには実現できません*12(これは、Sにおいてエッジは3点交換になっていて偶置換であるということに由来します)。したがってケース1は3点交換とみなして解決し、ケース2は敢えて4点交換(2つの隣接2点交換)とみなして解決します。

$E$ がRFに来るよう持ち替え
ケース1のとき
- あるエッジ $A$ を基準にすると3点交換に見える
- $A$ の対辺エッジを $B$ とすると、 $B$ の現在位置および $B$ が入るべき位置は隣接している
- それら2つがUBとURに移動するようU面を回転
- Sを1or2回実行し、 $B$ を目標位置に移動させる
- (この時点で $A$ と $B$ の2つのみが正しい位置に入っており、かつ $E$ の位置にはU面エッジが入っているはず。したがって残りはU面の隣接2点と $E$ の3点交換となる。)
- U面エッジのうち揃っていない2つがUBとURに来るようU面を回転
- Sを1~2回行うとU面エッジが全て揃う
ケース2のとき
- 上の手順の要領でU面エッジの3点交換が実現可能であり、隣接2点交換任意の向きで任意の3点交換を実行するとケース1の状況になることが分かる。
- 具体的には、SU’Sで3点交換が実現できるので、向きを気にせずコレを実行すればよい。(U’はUFがURに行くようなU面の回転)

(3)すると実は全エッジが揃っている

改めて現在の状況を分析し直すと、

下二段は $K$ (RFD)、 $E$ (RF)以外全て揃っていて、　
今U面エッジ4つを揃えた

ので、揃っていないパーツをエッジとコーナーに分けて考えると、エッジは $E$ 1つだけ、コーナーは $K$ とU面コーナー4つで合わせて5つ残っていることになります。しかし、 $E$ 以外の11個のエッジは既に揃っているので、少なくとも $E$ は本来入るべき位置に既に入っていることが分かります。さらに前編で考察したエッジの向きに関する不変量 $flip$ を思い出すと、最初の状態 $x$ が $flip(x)=0$ を満たすことを仮定すれば現在も $flip$ は0であって、 $E$ 以外のエッジは全て正しい向きで入っているので、 $E$ も正しい向きであり、すなわちもはや全てのエッジが揃っているのです。

5.残りコーナー5個を揃える

残すはコーナー5個のみ。8355の「妙」、ご覧あれ。

(1)D面を揃える

突然ですが、まずキューブ全体をひっくり返します。今までU面だった面がD面になるようにし、 $K$ をRUFに合わせます。これで揃っていないコーナーはRUFにいる $K$ とD面のコーナー4つとなります。
ここから、SとD面の回転を使ってコーナーを動かしていきます。多分以下の手順を実行すると「え？？」となると思うのですが、とりあえず書きます。

D面に入るべきコーナーで、揃っていないもの $X$ をとる
がRUFにあるとき、(の位置)
- $X$ が入るべき位置を $L$ として、
- $L$ がRFDに来るようにD面を回転
- $X$ が正しい向きで入るまでSを繰り返す
- (D面を回転させて向きを戻す)
がD面にあるとき、
- $X$ が位置RFDに来るようにD面を回転
- Sを1回行うと $X$ がRUFに来る

(2)残り2個まで揃える

ここまで読んだ方なら「2.D面コーナーを揃える」のステップと同じ要領で(現在の)D面コーナー4点が揃えられることは了解されると思います。が、問題はすでに揃えたパーツたちが崩れまくっているということです。しかし、よーく考えると、崩れているように見える部分は思ったほど崩れてはいないということが分かります。Sの性質をよく思い出す必要があるので、図を再掲しておきます。

現在揃っていないパーツは以下で全てである。
- FR,UR,UBの3つのエッジ
- RUF,RUB,LUBの3つのコーナー
コーナーRUB,LUB(図の青部分)は揃った状態から何回かのSで動いただけなので、Sの性質より合計回数が6の倍数になるまでSを実行すれば揃う
エッジFR,UR,UB(図の黄・緑部分)もS以外で動かされていないので、Sの性質より合計回数が3の倍数になるまでSを実行すれば揃う
以上から、Sを何回か実行すれば上記の5パーツが全て揃う。
この過程でRUF,RFD(図の赤部分)は崩れるので、揃っていないのはこの2つのコーナーだけとなる。

というわけで、残りコーナー2個のみの状態にできました。8355 method全体において、このトリックが一番「かしこい！！」と思える部分ですね。なお、ここまでのステップに沿って実際にキューブを揃えていると、運が良ければ*13既に揃っているということもあります。

(3)最後の2個を揃える

ラストです。もうあり得る状態があまりにも少ないので、総当たりをしてしまいます。

まずは現状の整理から。RUFとRFDのコーナー2つ以外は全て揃っています。ここで、前編で考察した位置に関する不変量 $sgn$ 、コーナーの向きに関する不変量 $pivot$ 、そして当初の仮定「最初の状態 $x$ は $sgn(x)=1,pivot(x)=0$ を満たす」を思い出すと、

$sgn$ の値から2つのコーナーの位置は合っている
$pivot$ の値から2つのコーナーの回転値の合計は0

ということが分かります。以上をまとめると、現状パーツのあり得る状態は(既に揃っているというものを除いて)

ケース1: RUFが右に、RFDが左にピボットしている
ケース2: RUFが左に、RFDが右にピボットしている

という、以下の2つの図しかないことになります。(D面は白だと考えてください)

f:id:goldenfalcon496:20200331011613p:plain — 最終局面の状況1

f:id:goldenfalcon496:20200331011647p:plain — 最終局面の状況2

結果から言うといずれの場合でも処置はほとんど同じですので、まとめて考えます。まず、(またしても)ピボットしている2つのパーツがRFDとLFDの位置に来るようにキューブの向きを変えます。この状況から再びステップ(1)D面コーナーを揃える を実行することを考えます。

すると、RFDとLFDのコーナーを揃えるためにそれぞれSを何回か実行することになりますが、それは具体的に何回でしょうか。まず、「実行するごとにコーナーの位置が入れ替わる」という特性上、RFD,LFDの両者とも実行されるSの回数は偶数です。さらに、「コーナーが全ての向きを実現しながら遷移する」ことを考えると、RFDとLFDはピボットしている向きが異なるので、どちらか一方は2回、他方は4回のSの実行で揃うということが特定されます。

ステップ(2)での、D面とRFD以外のパーツはSのみで動いている(ので思ったほど崩れていない)という議論を思い出すと、今再びステップ(1)に沿ってSを6回実行しつつD面を揃えたので、Sに影響されるRUF,RFD以外のパーツは全て元に戻っています。そしてRUFの動きを注意深く追うか、仮定 $pivot(x)=0$ を再び使えばRUFも正しい向きで入っているということになり、以上を総括すると、

RFDとLFDのコーナーのみが揃っていないとき、(S2回)D(S4回)D’または(S4回)D(S2回)D’で全てのパーツが揃う
(ただし、DはFDがRDに行くようなD面の回転、D’はその逆)

ことが示されます。NKT...*14

まとめ

本流の「証明」の流れを思い出しながら、終わりの部分を書きます。

前編で、

キューブのパーツ配置に対しいくつかの量が定義できること
キューブの適当なパーツ配置 $x$ のうち、ある条件 $P(x) := sgn(x)=1, pivot(x)=flip(x)=0$ を満たすものは全体の $\frac{1}{12}$ しかなく、それ以外は”あり得ない”状態であること

を示してきました。そして後編のここまでで、条件 $P(x)$ を満たす配置 $x$ は全て揃えられる、すなわち”あり得る”状態であることを示しました。以上をもって、我々は以下の事実を自信を持って導くことができます。

ルービックキューブにおける、”あり得る”(6つの面の回転の組み合わせで揃えることができる)キューブの状態数は、全てのパーツ配置の数のちょうど $\frac{1}{12}$ であり、その総数は $43,252,003,274,489,856,000$ である。

$Q. \, E. \, D.$

あとがきとか補足とか

ここまでグッダグダな記事に付き合って頂いた皆様(実在するのか？)、お疲れ様でした…。とりあえず「1時間で分かる」は嘘かもしれないと思い始めたところです。学徒らしくきっちり無から説明をしていこうと思ったら想像よりはるかにたいへんでした。というか日本語力足りてなくないか。もっと日本語を書け。

そんな愚痴はさておき、多分この記事、実際にモノ(キューブ)が手元にないと分かりやすさ面白さが半減だと思います。ぜひ手にとって遊んでください。通販でまあまあなものが500~3000円くらい*15で買えます。ちゃんと理論通りに揃うという快感もあるし、何度か揃えればきっとタイムアタックをしたい気分になってきます。たぶん。
高速化を考えだすと全く違った世界が見えてきます。例えば、今回書いた解法にも、Sの「逆再生」も交えて解いていく*16などといった工夫の余地はたくさん残されていて、20秒程度のタイムまで出せると言われています*17。1個買ったら高々数千円で1年遊べる、小ネタにもなる、ちょっと賢く見える*18、楽しいおもちゃ。この機会に手にとってみてはどうでしょう。

と、雑な布教をして終わります。ありがとうございました。

*1:そうでないものもあるのかもしれませんが、とてもマイナーだと思います。筆者の記憶にはないです。なお、後述する8355は結構イレギュラーですがこの原則は守られていると考えています

*2:実際、最近のキューブ競技の"研究"においては、より効果的な操作を編み出すべく人力ではなく計算機による探索が行われています

*3:この名前は揃えるパーツの個数を順に並べたものです。D面コーナー1つを除くD面パーツ8個→中段エッジ3個→残りエッジ5個→残りコーナー5個。

*4:具体的にはステップ4(3)と5(3)で仮定を使います

*5:実は一般に操作A,Bに対してABA'B'と表される操作の特性が一部の分野で重要な研究テーマになっています。詳細はコミュテーターで検索

*6:記号Sを用いるのは、なぜかこの操作がSexy moveと呼ばれていることによります。一応、キューブ界隈の標準的回転記号ではSは別の操作を表すのですが、気にしないことにします

*7:鋭い方はお気づきでしょうが、必要な操作の量はとてもかさみます。この解法は全くもってスピードに向いていません！

*8:キューブ全体の向きを変える操作にも回転記号が割り当てられています。この記事での「持ち替え」はy,y’などが対応し、これはy軸まわりの回転という意味です。

*9:最後まで読むと、本当に最後の最後であることが分かります

*10:前編で定義したエッジの基準の向きを用いると、基準の向きになっているエッジだけがSやSSで揃えられるということが分かります。一方、90˚の持ち替えをすると中段エッジに関しては基準の向きが逆転するので、うまく持ち替えをすれば目的エッジを基準の向きにできます。しかし、このとき目的の位置がRF(Sで移動できる範囲)に来るとは限らず、LFに持ってきて鏡映操作をすることでなんとかなります。

*11:回転記号ではUwなどと書かれます

*12:これはかなり曖昧な物言いです。正確には、『作業の合間でのU面の回転角度の合計を0に保って2点交換することはできない』となります。実際、U面の回転は4点の巡回置換すなわち奇置換であり、そのおかげでこのステップにおける(見かけ上の)2点交換が成立しているのです。

*13:この確率は、最終ステップで示す揃っていない2パターンと同様に確からしい気がするので？1/3であると考えられています。

*14:長く苦しい戦いだった…

*15:速さと快適さを求めて技術革新が進んでおり、高いものは高いです。でも3000円以下の範囲で割と十分だと考えています。

*16:もう少し説明すると、Sは6回実行すると元に戻るので、Sを5回実行する代わりにSの逆再生を1回実行した方が速いといったケースはありますが、今回の説明では「何度かやれば揃う」としか言っておらず、実際に何回やれば良いかを実行前に見極め、適切な処置を取るのは至難の業です

*17:こんな解法よりはるかに速いと言われるメジャーな解法を用いて筆者が本気を出すと20秒くらいになります。おい。

*18:スピードキューバーになると分かってしまうのですが、競技キューブは賢さの問題ではありません。これはれっきとしたスポーツです。

496の落書き帳

496がなんか思ったことを書いたり書かなかったりする場所です。

ルービックキューブの状態の総数が43,252,003,274,489,856,000通りであることの証明(ルービックキューブが1時間で揃えられるようになる方法付き)(後編)

もくじ